【2025年】東京科学大学の入試｜数学参考書ルート

本記事は高校１年生から浪人生まで、東京科学大学の理工学系合格を目指す受験生に向けて、数学入試攻略＋数学参考書のおすすめルートを紹介します！

東京科学大学は、2024年度に東京工業大学と東京医科歯科大学が合併してできた大学です。
入試は理工学系と医歯学系に分かれています。
理工学系の数学は東工大時代と変わらず、東京大学と同程度の難度です。

理工学系を目指す受験生は、しっかり数学対策を行っていきましょう！

東京科学大学の数学とは

試験の構成と出題内容

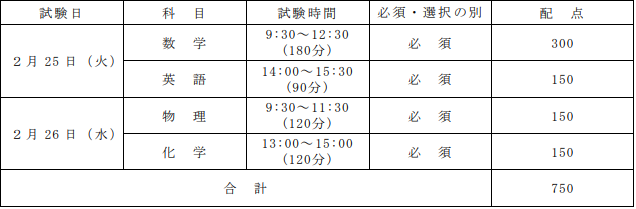
(東京科学大学　令和６年度一般選抜（前期日程）学生募集要項)

数学は、180分で300点満点です。
基本的に大問が５問あり、全問記述式です。単純計算で１問あたり約３５分考えることができます。

試験範囲は、数Ⅰ、数A(図形の性質、場合の数と確率)、数Ⅱ、数B(数列)、数Ⅲ、数C(ベクトル、平面上の曲線と複素数平面)となっています。

特徴

科学大の数学入試は、東京大学と匹敵するほどの最高難易度です。
難易度が上がる理由としては、大きく分けて２つあります。

まずは問題そのものの難しさです。

そしてもう１つが、試験時間の長さです。

科学大の数学は３時間(180分)と、一般入試としては最長の試験時間です(小論文等を除く)。
初めての場所で１人、普段と異なる机と椅子、本番というプレッシャーなどで緊張しながら、３時間手を動かし続けるというのは、想像以上にメンタルとフィジカルが求められます。

もちろんトイレ等の途中退室は可能なので、座り続けることがつらい人や、集中力が持たない人は気分転換を行うのも重要な戦略です。

また試験時間が長いため、分からない問題にも時間をかけることができます。
しかし前述したように、試験ではどのように解くか分からない問題しか出題されません。
分からない１問に時間をかけ過ぎていると、完答できたかもしれない問題を取りこぼす可能性もあります。

時間配分の戦略、自分の得意・苦手分野を見極める冷静な判断力、そして最後まで解けなくても次の問題に進む勇気が必要です。

数学の立ち位置

共通テストの点数は第一段階選抜(足切り)でしか用いられず、合否は２次試験の結果だけで決まります。
数学は他の科目より配点が高いため、数学の点数が合否を左右します。

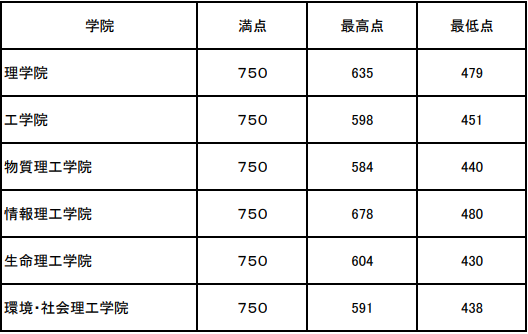
（東京科学大学　令和７年度一般選抜（前期日程）合格者学院別得点)

合格最低点を確認すると、4教科で450点前後となっています。
この450点を数学・英語・物理・化学でどのように配分するか、というのも大事な戦略です。

合格に必要な数学力

東京科学大学に特化した「数学力」の定義

科学大の数学入試の採点・評価基準には、
「確かな計算力を伴った論理的思考力があり、さらにそれが的確に記述できるかを問う」
とあります。
これをもう少し具体的にすると、以下のようになります。

それぞれの伸ばし方は、後ほど解説します。

偏差値の目安

模試での目標偏差値は、ボーダーラインが65〜67程度です。
70以上は安定圏に入ります。

模試の結果をどう読むか

模試の結果が返ってくると、一番気になるのが偏差値です。
偏差値によって判定も変わり、A判定だと自信が、E判定だと焦りが生まれるでしょう。

しかし東京科学大学を目指すのであれば、偏差値だけでなく、「答案の記述内容」「部分点が取れているか」に注目してください。
同じ偏差値でも「マークシート式」と「記述式」では後者が重要です。

東京科学大学の数学入試の特徴として、「全問記述式」「部分点で点を積み上げる」ことが挙げられます。
この２点に対応する力を確認するには、答えだけを記入するマークシート式ではなく、計算や思考の過程も記入する記述式での模試がより適切です。

そのため、偏差値や判定を参考にする場合は、記述式の模試を重視してください。

高校２年生の模試については、出題範囲に注意してください。

数２Bまで含めた出題による偏差値60と、数ⅠAのみ出題での偏差値60では信頼性が異なります。
よく勉強した数ⅠAだけの偏差値と、授業で学んだばかりの数ⅡBも含まれた偏差値では、数ⅡBも含まれた結果のほうが、より正確に実力を反映しているでしょう。
模試の結果で志望校を決める場合には、出題範囲も配慮して検討しましょう。

模試で点数が取れなくても合格することは十分あり得るので、

を意識して模試を受けてくださいね。

学習計画の立て方：全体のスケジュール感

東京科学大学ならではの勉強法

「答案構成力」の重要性

実際の入試では、全５問をすべて完答することはほとんどありません。部分点で点数を積み上げていくことになります。
数字が間違っていたり式が立てられていなくても、方針・途中式・補題の提示などが論理的に書かれていればしっかりと点数が与えられます。

逆に正解にたどり着いていても、論理が飛んでいたり、説明不足であったり、根拠があいまいな場合は減点されます。

また、採点者は答案内容の解釈や推察はしてくれないので、模試や定期試験では許されていた省略や式だけを並べた記述が、本番では減点ということもあります。

つまり答案構成力とは、
自分が何を考え、どう問題に取り組もうとしているかを採点者が読めるように、必要な情報を必要な順番で書く力
のことです。

気を付けるべきポイントは、

を守って記述できているかです。
普段からこのポイントを守り、論理的な記述を練習しておきましょう。

単なる公式暗記・解法暗記では戦えない

過去問を見ると分かりますが、誘導が少ないため、自分で方針を考えて解いていく必要があります。
そのためには、なんとなくの公式理解や、ただ覚えただけの解法暗記では不十分です。

(東京科学大学　過去の「入試問題」及び「出題の意図等」　理工学系　2025年度　前期日程)

方針を立てるには、筋道を立てて考え、根拠に基づいて結論を導くという論理力と、発想が必要になります。

根拠には、公式の意味や、問題に公式を使う理由が求められます。

また発想は、なにも無いところからは生まれません。様々な解法パターンと、解法を生み出す思考パターンがあることで、本番でもひらめくことができます。

徹底した公式理解や解法暗記は、普段の勉強から意識する必要があります。

計算力は絶対に裏切らない武器である

実際の試験では、分からない問題に対して様々な解法を試していくことになります。
その際に必要になるのが計算力です。

計算力とは、計算スピードと正確さ、そして正確な検算ができる力のことです。

どんなに解法を暗記し公式や定義を理解しても、計算スピードが遅すぎれば試行錯誤の時間が足りません。
ケアレスミスがあると間違った数字を解としてしまい、その後の展開が変わってきます。

また、検算が不正確だとケアレスミスのリカバリーができないまま減点になったり、「これであってるかな？」という不安を抱えたまま問題を解いていくことになります。

他大併願者と差がつくポイントとは？

他大学と科学大の数学における大きな違いとは、どこから手を付けていいかわからない初見問題が出題される、という点です。
このような問題に粘り強く取り組めるか、が他大併願者との差が付くポイントになります。

科学大の数学における粘り強さとは、問題へアプローチする際の手数の多さです。
この手数を増やすには、実験や視覚化ができるようになる必要があります。

実験は、複雑な問題を簡単な構造や知っているパターンに分解する、知っている定理や公式が使えるか小さな数字で試してみる、といった問題を観察し、知っている解法を試してみるということです。

視覚化は、場合の数を表や樹形図で書いてみる、関数をグラフにしてみるなど、複雑な問題や混乱しがちな思考を、見える形にして理解する工夫のことです。

実験や視覚化をとりあえずやってみることが、初見問題で手が動かない状況から抜け出すきっかけになります。

数学参考書ルートマップ

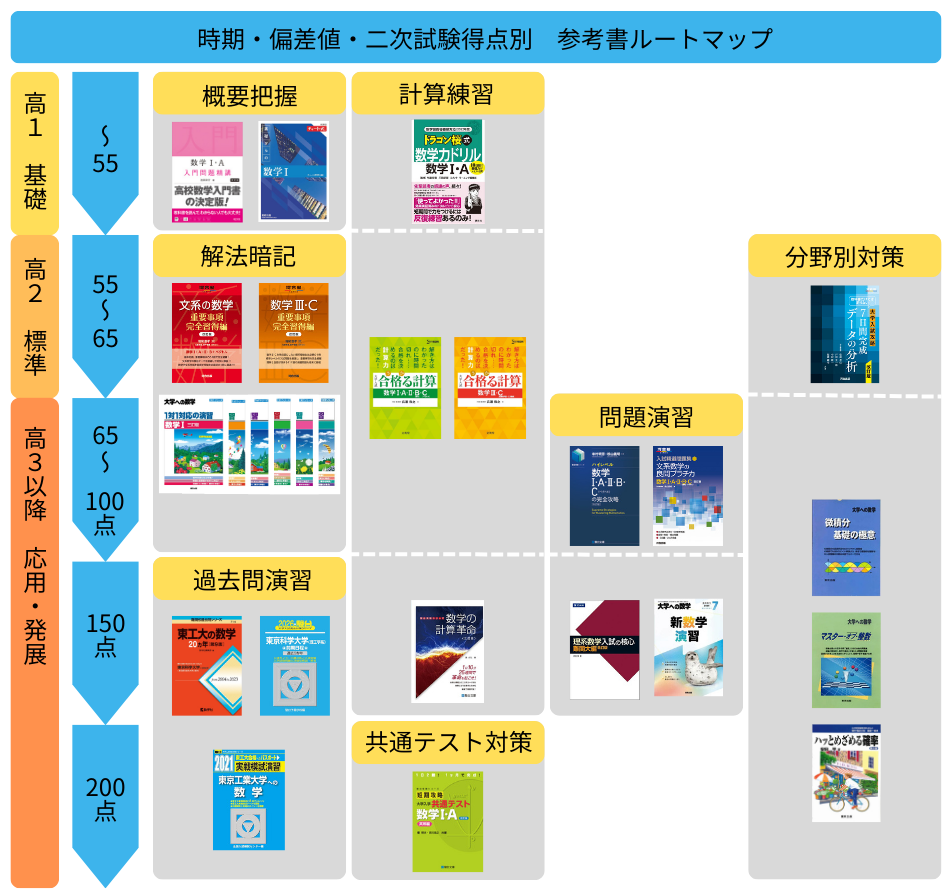
基礎（偏差値：〜55）

基礎概要把握

数学の単元を一通り学習する、定理や公式を定着させるための学習です。

おすすめの参考書は、「入門問題精講」、もしくは「青チャート」です。
実際に手に取ってみて、使いやすさや解説の読みやすさなどで選んでください。
どちらも範囲別でまとめられているので、ⅡBとⅢCも忘れないようにしましょう。

修了基準は、例題が自力で7割以上解けるかが目安です。
解けるようになったら、次の段階に進みましょう。

基礎計算練習

計算練習は、入門問題精講や青チャートで公式などを学んでから行いましょう。
学んだ公式を使って計算問題を解いていきます。

教科書レベルの計算練習には、「ドラゴン桜式計算ドリル」がおすすめです。
時間を測って取り組み、前回より早く解けるよう記録しておきましょう。

標準問題のマスター（偏差値：55〜65）

解法暗記

「解法の引き出し」を持てるようになるため、典型的な解法を用いた問題を解く段階です。
概要把握を行った後に取り組んでください。

まずは、「文系の数学重要事項完全習得編」・「数学III重要事項完全習得編」で基本的な解法を学びましょう。
目標は２～３ヶ月で２冊を２周です。

「入門問題精講」、「青チャート」からいきなり「一対一対応の演習」にいくとハードルが上がりすぎるため、この２冊で基礎を学んでおくとよいでしょう。

修了基準は、「解法の理由を説明できるようになる」ことです。

科学大対策では、「一対一対応の演習」が必須です。
６か月で６冊を2周することが理想のため時間がかかりますが、科学大対策に必要な解法をすべて網羅することができます。
高２から高３春までには終わるように、計画を立てて取り組んでいきましょう。

計算練習

入試によく出る計算処理を練習するには、「合格る計算ⅠAⅡBC」・「合格る計算ⅢC」がおすすめです。
まずは正答率60%を目指して取り組みましょう。

分野別対策

データの分析単元が苦手であれば、「7日間完成データの分析」で弱点補強を行いましょう。

応用力・記述力の養成（偏差値：65〜）

応用問題演習 （100点以上を目指す）

「一対一対応の演習」で身に着けた解法を、実際に応用していく段階です。
「ハイレベル数学の完全攻略」・「ハイレベル数学の完全攻略ⅢC」は１問につき解説が３ページ以上と充実しており、類題も掲載されているため、解法の幅を広げるのに最適な参考書です。

「ハイレベル数学の完全攻略」が向いていない、と感じる人には、「文系数学の良問プラチカIAIIBC」・「文系数学の良問プラチカIIIC」もおすすめです。
難易度はほとんど変わらないので、好みで選んでも大丈夫です。

発展問題演習（150点以上を目指す）

「理系数学 入試の核心 難関大編」は応用性の高い良問を集めた、コンパクトな参考書です。
微分積分、図形、整数を重視した問題選びになっています。

「新数学演習」は難易度が高く発想力が求められる問題です。
数学で高得点を取りたい人におすすめの参考書です。
１問を考えるのにかなりの時間が必要なため、他科目の対策も万全で、さらに上を目指す場合にだけ使いましょう。

応用計算練習（100点以上を目指す）

科学大の数学に対応するために、高３以降は「合格る計算ⅠAⅡBC」・「合格る計算ⅢC」で正答率80％を目指してください。

応用分野別対策（100点以上を目指す）

「場合の数」「確率」の単元が苦手であれば、「ハッと目覚める確率」がおすすめです。
解説にユーモアが交えられており、楽しく解ける・読める参考書です。
現行課程には対応しておらず、読み飛ばしが必要が箇所もあるので注意が必要です。

発展分野別対策（150点以上を目指す）

「マスター・オブ・整数」は、まさしく整数の単元をマスターするためにおすすめの参考書です。
解説が詳しく、整数問題への様々なアプローチ方法を学ぶことができます。
４章は数学オリンピックレベルなので、入試までの残り時間と相談しながら２章まで、３章までと区切りながら使うのもよいでしょう。

科学大では微分積分は頻出の単元です。
「微積分基礎の極意」をやりきれば、ほとんどの微積分問題に対応できるようになるため、科学大対策では必須級の参考書です。

発展計算練習（150点以上を目指す）

「数学の計算革命」は、計算処理をより高度に、より短時間で行えるようにするための参考書です。
制限時間がA・Bとあり、数学を得点源にしたい人は、より時間の短い制限時間Aで解ききることを目指してください。

共通テスト対策

共通テスト形式の実践には、「短期攻略大学入学共通テスト ⅠA実践編」・「ⅡBC実践編」がおすすめです。
大問単位の演習ができ、穴埋め形式に慣れることができます。
共通テスト模試などで不安を感じた場合に使用するとよいでしょう。

過去問

赤本・青本が代表的な過去問です。

赤本は、過去の入試情報や合格体験記が掲載されており、周辺情報が豊富です。
赤本シリーズ（東京科学大学５カ年）と、難関校過去問シリーズ（東工大の数学20カ年）では解説の内容が異なるので、読み比べるのも良いと思います。

青本は駿台が出版しており、解説が正確で丁寧です。
発想や別解も掲載されているので、特別な理由がない限りは青本を使用しましょう。

過去問が一段落ついた人には、「東工大実践問題」もおすすめです。
絶版している本ですが、形式が実際の入試と似ているので演習量を積みたい人におすすめです。
学校の進路指導室や予備校にある人は使ってみてください。

過去問の使い方 ― 合格点を取るための実戦力

基本的な過去問の使い方

東京科学大学の特徴に合わせた数学力を伸ばすために、過去問を使いましょう！

傾向を掴むためにも、過去20年分は解きましょう！

時期別の活用法

共通テスト対策

目標得点ライン：90点を目指すべき？

第一段階選抜では、理工学系全体の倍率が４倍になるようボーダーが設定されます。
足切りされないために合計で８割は必要でしょう。
国語や社会系などの文系科目に不安がある場合は、数学で90点以上を目指しましょう。

(東京工業大学　令和６年度一般選抜（前期日程）学生募集要項)

二次試験対策との両立

共通テストは二次試験と比べ問題文が長く複雑なため、問題の把握に時間がかかります。
文章を読む時間や、考える時間の確保のために計算スピードが求められます。
また各分野からまんべんなく出題されるため、得意な分野から解いていくなどの戦略も必要です。

数学以外の科目で点数を落とし足切りされないよう、冬ごろからは他科目の共通テスト対策も行っていきましょう！

最速で数学150点を取るには　―最短参考書ルート

• 数学はそこそこの得点で他科目で点数を取り合格を目指す人、
• 高３から科学大対策を始める人

に向けた、最短の参考書ルートです。

必ずやるべき「概要把握」と「解法暗記」を押さえ、「過去問」で演習を行います。
「一対一対応の演習」から「過去問」にいきなり進むとハードルが上がりすぎるので、「ハイレベル数学の完全攻略」を挟むのがおすすめです。

数学が得点源ではなくても、他の科目で点数をしっかり取れれば合格は狙えます！
時間がなくてもあきらめず、やれることをやっていきましょう。

まとめ

数学はとにかく、基礎を徹底して積み重ねることが大事です。

そして、東京科学大学は進学してからもずっと数学が必要です！
大学での授業のためにも、ぜひ今のうちに数学力をつけておきましょう。

受験勉強のモチベーションのために、受験勉強の数学がどのように大学数学につながっていくかを調べるのもおすすめです！

監修

現論会ジャーナル編集長 寺田貴博

開成中学校・高等学校を経て東京大学農学部を卒業。
現論会を運営する株式会社言楽舎の取締役。
「大学受験参考書を知り尽くしたコーチング指導のプロ」として、日々難関大受験生の自学自走と第一志望校合格をサポートしている。