【化学の基本！】化学・構造式の基本と書き方！

化学基礎の序盤で学ぶ構造式。

特に化学を学び始めた段階の人は様々な結合の表し方が登場し混乱している人も多いかと思います。

そこでこの記事では構造式とは何か、どのように書いたらいいかを解説していきます！

構造式とは

高校化学では電子式など様々な結合の表し方を学んできました。

構造式はそのような化学の結合を表す1つの書き方です！

特徴としては結合に使われている電子に焦点を当てて書かれている点です。

構造式のイメージと書き方

ここでは例として水分子について考えましょう。

水分子は酸素原子1つに水素原子2つが共有結合した物質です。

それぞれの電子式は以下のようになります！

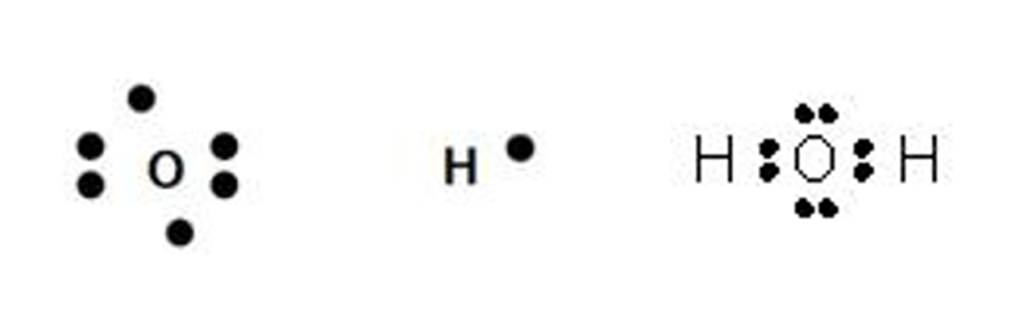
この図のように酸素原子は2つの不対電子を、水素原子はそれぞれ1つの不対電子を持っています。

酸素原子の不対電子が2つの水素原子の不対電子とそれぞれ共有結合することで、水分子となります。

こうすることで原子の最外殻電子がすべて電子対となり原子として安定の電子配置となります！

安定な電子配置というのは、普通の原子だと電子が8個で電子対が4個の時、水素とヘリウムの場合は電子が2つで電子対が1個の時のことです！

それでは、それぞれの原子を構造式で書くと以下のようになります！

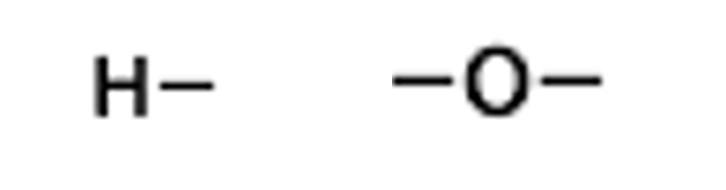
見ていただくとわかると思うのですが酸素原子からは2本、水素原子からはそれぞれ1本ずつ線が出ています。

この線のことを価標といいます！そして価標の数のことを原子価といいます！

この場合では、水素の原子価は1、酸素の原子価は2ということになります！

ところで、この原子価は電子式で水分子について考えた時にどこかで出てきた数字です。さてどこで出てきたのでしょうか。

・

・

・

・

そう不対電子の時に出てきましたね！

冒頭で述べましたように構造式は結合に焦点を当てた分子の表し方です。

酸素原子は不対電子が2個、水素原子は1個。これに価標が対応しています。

このまま水分子の構造式を作ると以下のようになります。

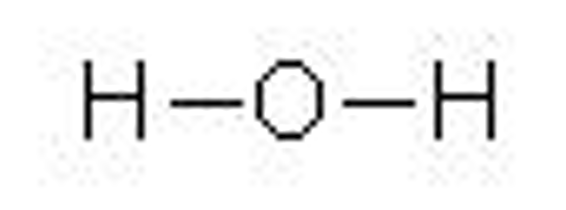
酸素原子の価標の1つが水素原子の価標の1つと結びついて1本になりました。

ここで価標の本数が前と後で同じになるように2重に書いてしまう人が時々いるのですが、それはNGです。

価標の1本ずつをむずび合わせて新たな1本になります。

この結合の本数は単結合、二重結合、三重結合となるにつれて1本、2本、3本と多くなっていきます！

配位結合

まずは配位結合とは何かをおさらいしていきます。

今まで見てきた共有結合は2つの原子がお互いに電子を出し合ってペアを作っていました。

ところが、結合には片方の原子の電子対をもう一方の原子の空いているところにペアごと出してあげることがあります。

これが配位結合です。

共有結合よりは不安定な形ですが立派な結合の一種です。

この配位結合を表すときは矢印を使うことがあります。

一例としては以下のようなものです

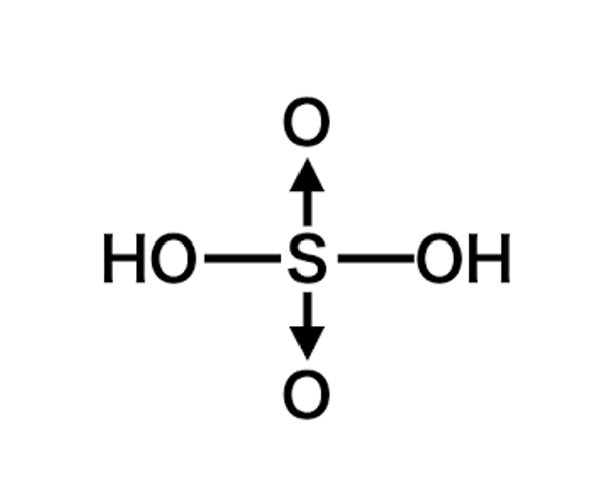
この構造式はあの硫酸の構造式です。

硫黄原子は2つの酸素原子と共有結合して、もう2つの酸素原子とは配位結合していることを示します。

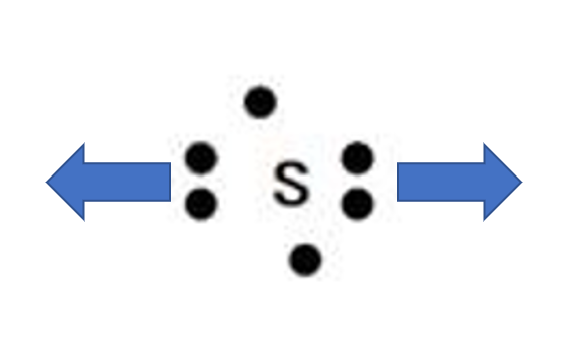
硫黄の部分だけ切り出すとこのようになります。

なぜこのような図を出したかというと、多くの人が矢印の向きが分からなくなってしまうからです。

入試で時折求められる配位結合を含む構造式を書くときはこの図のようなイメージを持って解答してもらえたらと思います！

この記事に関連したオススメ記事

オススメ第１位：【2020年最新版】東大生おすすめ！化学の成績が上がる問題集3選！

オススメ第２位：【ゼロから独学！】化学を独学するための勉強計画を一挙公開！

オススメ第３位：【化学勉強ルート完全版】化学の偏差値を30上げる化学の勉強法とは？