「がむしゃらな勉強」はもう卒業。大学受験に必須の「ロジカルシンキング」とは?具体例で解説
更新日 : 2025年11月22日

はじめに:成績が伸び悩む原因は「論理」の欠如?
「毎日机に向かっているのに成績が上がらない」 「何をどれくらい勉強すればいいのか不安になる」
受験生の多くが抱えるこの悩み。実は、能力の問題ではなく、「考え方(思考プロセス)」に原因があることが多いのです。
ビジネスの世界では、問題解決のために「ロジカルシンキング(論理的思考)」が必須とされていますが、これは大学受験においても極めて強力な武器になります。
今回は、現論会が大切にしている「論理的な勉強計画」の基礎となる考え方を、ビジネスのフレームワークを応用して具体的に解説します。
受験勉強におけるロジカルシンキングとは?
ロジカルシンキングとは、物事を体系的に整理し、筋道を立てて矛盾なく考える思考法のことです。これを大学受験に当てはめると、以下のようになります。
- 感覚的な勉強:「なんとなく不安だから、今日はこの参考書をやろう」
- 論理的な勉強:「志望校合格というゴールから逆算すると、今月は基礎固めが必要。だから今日はこの単元の復習を完了させる」
感情やその場の気分に流されず、「合格」というゴールに向かって最短距離を走るための思考法、それが受験におけるロジカルシンキングです。
具体例で実践!受験に使える思考フレームワーク
ご提示いただいた参考記事にもある「MECE(ミーシー)」や「ロジックツリー」といった考え方は、そのまま受験計画にも応用できます。具体的なシーンで見てみましょう。
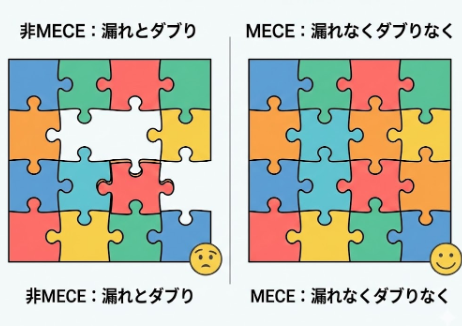
1. 漏れなくダブりなく(MECE)で現状を整理する
MECE(Mutually Exclusive and Collectively Exhaustive)とは、「漏れがなく、ダブりもない」状態のことです。
【悪い例:MECEではない状態】
- 英単語帳を3冊買っけれど、どれも中途半端。
- 「長文読解」ばかりやって、「文法」が抜けている。
これでは、知識に穴(漏れ)があったり、同じ範囲を無駄に繰り返して時間ロス(ダブり)が発生したりします。
【良い例:MECEな状態】
- 志望校のレベルに必要な単語数は2000語。
- それをカバーする単語帳は『〇〇』1冊で十分。
- この1冊を完璧にすれば「漏れ」も「ダブり」もない。
現論会では、志望校合格に必要な要素をすべて洗い出し、無駄な重複を削ぎ落としたカリキュラムを作成しています。これが「最短ルート」の正体です。
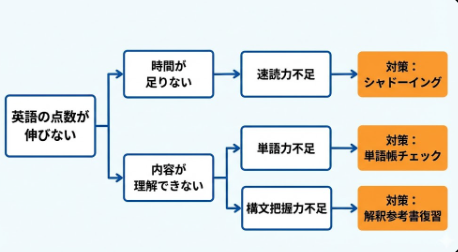
2. ロジックツリーで「成績が上がらない原因」を深掘りする
模試の結果が悪かったとき、「もっと頑張ろう」という精神論だけで済ませていませんか? ロジックツリーを使って、原因を具体的に分解することが重要です。
【例:英語の点数が伸びない場合】
- なぜ英語ができない?
- 時間が足りないから?
- 速読力が不足している?
- → シャドーイングを取り入れよう
- 速読力が不足している?
- 内容が理解できないから?
- 単語がわからない?
- → 単語帳の完成度をチェックしよう
- 構文が取れていない?
- → 解釈の参考書を復習しよう
- 単語がわからない?
- 時間が足りないから?
このように、「なぜ?」を繰り返して要素を分解していくことで、「今、自分が何をすべきか」が明確になります。これをせずになんとなく勉強しても、穴の空いたバケツに水を注ぐようなものです。
感情に頼らず、事実とデータで計画を立てる
ロジカルシンキングにおいて重要なのは、客観的な「事実」に基づいていることです。
- 「たぶんできるはず」という希望的観測
- 「友達がやっているから」という同調行動
これらは論理的ではありません。
- 「過去問で〇〇点が取れていない(事実)」
- 「合格最低点まであと〇〇点必要(事実)」
- 「残りの日数は〇〇日(事実)」
この事実に基づいて、「1日あたり何ページ進める必要があるか」を割り出すのが、現論会のスタンスです。
まとめ:論理的な計画が、不安を消し去る
「これで間に合うのだろうか?」という受験特有の不安は、計画が曖昧だからこそ生まれます。 ロジカルシンキングを用いて、やるべきことが明確(MECE)になり、弱点の原因が特定(ロジックツリー)できていれば、あとは「やるだけ」の状態になります。
迷いがなくなれば、勉強の密度は劇的に上がります。
あなただけの「論理的な学習計画」を作成します
とはいえ、自分一人で客観的に現状を分析し、完璧な計画を立てるのは難しいものです。
現論会では、一人ひとりの志望校と現状の学力に合わせて、「何を、いつまでに、どのようにやるか」を論理的に組み立てたオーダーメイドの計画を作成します。
「今のやり方で合っているのか不安」「無駄な勉強をしたくない」という方は、ぜひ一度、現論会の無料受験相談にお越しください。あなたの現状をロジカルに分析し、合格への最短ルートをご提示します。
