受験生なら誰もが経験する「手が止まる瞬間」

受験勉強を続けている皆さんなら、誰もが経験する瞬間があります。それは、模試や過去問、そして恐ろしいことに入試本番で、問題を見た瞬間に「全く解き方が分からない」「手がかりが一つも見つからない」と絶望する瞬間です。

どれだけ勉強を積み重ねても、未知の問題や難問は必ず現れます。先生自身も、「受験生みたいな生活を10年以上続けてきても、入試問題を見てゾッとする瞬間がある」と語っています。問題のパターンは広大であり、全てを網羅することは不可能だからです。

しかし、そこで諦めてはいけません。

この授業で先生が伝えたのは、「解き方が全く分からない」問題に出会った時、どういう思考プロセスで、何をすればいいのかという、最も実践的かつ強力な「対処法」です。これは単なるテクニックではなく、真の数学力を支える思考の技術です。

数学力をグッと高めるための3つの実戦的対処法、そして東大・千葉大の入試問題を用いた実践例、さらにメンタル面の最終奥義まで、詳しく見ていきましょう。

対処法【原則】：まず考えるべき「解かない」という最強の選択

解法を考える前に、まず皆さんが持っておくべき最も重要な心構えがあります。

原則1：解かなくていい！

全く分からない問題に出会った時、最初に考えるべきは「解かなくていい」ということです。

入試問題は、大問が4〜6問程度あることが一般的です。そして、皆さんが目指す大学の合格最低点を考えてみてください。多くの大学では、60%から65%程度が合格のボーダーラインとなっています。

つまり、全問正解する必要は全くないのです。

もし大問が5問あったとして、1問完全に解けなかったからといって不合格になるわけではありません。解き方すら全く分からない問題に何十分も費やし、結果として他の解ける問題に手が回らない、あるいは集中力が切れることこそが、最も避けるべき失敗です。

手がかりが全く見つからない場合は、一旦立ち止まり、その問題は解かないという選択をすることが、合格への最短ルートである場合が多々あります。

ただし、これを徹底すると、「これもやめよう、あれもやめよう」となり、結局1問も手をつけられないという事態になりかねません。そこで、ここからは「それでも解きたい」「なんとか食らいつきたい」と思った場合に、どう行動すべきかという実践的な話に移ります。

対処法【実践テクニック】：思考を深める3つのステップ

「解かない」という選択肢を頭に入れつつも、食らいつくための具体的な行動は以下の2つです。

原則2：具体例で考える（とにかく手を動かす）

難問に直面した時、頭の中で全てを解決しようとするのは非常に困難です。なぜ難しいと感じるかといえば、その多くは**「文字」（変数）が多すぎる**からです。

そこで、自分から問題を簡単な具体例に落とし込み、「実験」することが重要になります。

1. 問題のレベルを勝手に落とす
   • 文字（n,k,aなど）が入っていたら、自分で n=0,1,2 や a=0,1,−1 などの具体的な数値を代入してみましょう。
2. とにかく手を動かす
   • 入試本番では、特に緊張から手が止まりがちです。何も動かしていない状態では、脳もロックされ、良いアイデアは浮かびません。
   • 具体例で手を動かすことで、思わぬ法則性が見つかったり、解答への道筋がふと見えたりすることがあります。

数学が得意な受験生のノートを見ると、解答を書き始める前に、問題用紙の隅で色々と実験している様子がうかがえます。まずは手を動かす、そのための具体的な数値による実験が、最初の突破口となるのです。

原則3：問題の分割（場合分けを「する」）

本当に難しい入試問題は、単発で難しいというよりは、いくつかのそこそこ難しい基本問題が何層にも重なってできていることがほとんどです。

この難解な複合問題を解きほぐすために、意識的に行うのが**「問題の分割」、すなわち「場合分け」**です。

先生はここで、数学の得意な人と苦手な人の「場合分け」に対する決定的な考え方の違いを指摘しています。

• 苦手な人の考え方： 「うわ、場合分けの問題だ。また面倒なことをさせられるのか…」
• 得意な人の考え方： 「場合分けを望んでする！」

場合分けは、決して面倒な作業ではありません。難しい問題だからこそ、自分から場合分けのポイントを見つけ、問題を分割し、解ける部分を意図的に増やしに行くのです。

場合分けをすることで、複雑な問題がシンプルなケースに分かれ、手がつけやすくなります。さらに、部分点がつきやすくなるという大きなメリットもあります。たとえ最後の結論まで辿り着けなくても、ある特殊なケースで正しく議論できていれば、点数がもらえる可能性が高まるのです。

「場合分けをさせられる」のではなく、**「する場合分けがあるなら、喜んでしよう」**という心構えに変わるだけで、格段に問題に食らいつけるようになります。

実践例1：千葉大学の整数問題に挑む

これらの原則を、実際の難関大入試問題で実践してみましょう。

問題設定（千葉大学）

a^2+4a+12/8a+8​ が整数となる整数 a の値をすべて求めよ。（[14:45] 参照）

一見すると、どこから手をつけていいか分からない問題です。

1. 具体例で実験（法則性の発見）

まずは手を動かし、具体的な a の値を代入してみます。

• a=−1 のとき、分母は 1−4+12=9、分子は 8(−1)+8=0。よって 90​=0 で整数（OK）。
• a=2 のとき、分母は 4+8+12=24、分子は 8(2)+8=24。よって 24/24​=1 で整数（OK）。

この時点で、答えを2つ見つけることができました。しかし、法則性までは見えません。

そこで、**次数**に注目します。

• 分母： 2次式（a2 がある）
• 分子： 1次式（8a がある）

a の値が大きくなるほど、分母にある a2 の増加スピードが圧倒的に速くなります。例えば a=100 なら、分母は 10000 程度、分子は 800 程度となり、分数の値は0に近づき、決して整数にはなりそうにありません。

この実験から、「∣a∣ が大きい範囲には答えはない」という強力な法則性、すなわち絞り込みの方針が立ちます。

2. 必要条件による問題の分割（範囲の絞り込み）

方針が固まったら、次にこの**「∣a∣ が大きすぎない」という条件を数式で表現し、問題を分割**します。

分数が整数であるための必要条件は、**「分数の絶対値 ≥1」**でなければなりません（0の場合を除く）。

​a2+4a+128a+8​​≥1

分母は平方完成すると (a+2)2+8 となり、常に正なので絶対値は不要です。

∣8(a+1)∣≥a2+4a+12

ここで「場合分けをする」機会が訪れます。絶対値を外すために、a+1 の正負で場合分けします。

1. a≥−1 の場合（a+1≥0）：
   • 8(a+1)≥a^2+4a+12 を解くと、a^2−4a+4≤0、すなわち (a−2)2≤0 となります。
   • これを満たすのは、a=2 のみ。これは a≥−1 を満たし、最初に発見した答えの一つです。
2. a<−1 の場合（a+1<0）：
   • −8(a+1)≥a^2+4a+12 を解くと、a^2+12a+20≤0、すなわち (a+2)(a+10)≤0 となります。
   • これを満たすのは、−10≤a≤−2 です。
   • この範囲は a<−1 という条件を完全に満たしています。

結果として、答えとなる a は、最初に確認した**a=−1、そして絞り込んだ範囲−10≤a≤−2、さらにa=2**の範囲にしか存在しないことが分かりました。

3. 結論

絞り込んだ範囲（−10,−9,…,−2,2,−1）の整数を、全部で9通り（a=−1 と a=2 を含む11通り）検証すれば終了です。

実際に代入して確認すると、整数値を取るのは以下の5つに限定されます。

a=−10,−4,−2,−1,2

教訓： 難問でも、具体例による実験と、場合分けによる分割を行うことで、必ず手がかかりが見つかり、やがては「調べ尽くせる範囲」に問題を落とし込むことができるのです。

実践例2：東京大学の確率問題に挑む

もう一つ、さらに難易度の高い問題で、問題の分割と見落としがちな条件の利用を実践します。

問題設定（東京大学）

3×3の9つの部屋があり、最初Pにボールがある。1秒ごとに隣の部屋へ等確率で移動するとき、N 秒後にQの部屋にいる確率を求めよ。（[40:06] 参照）

1. 具体例で実験（偶奇性と対称性の発見）

「N 秒後」という文字が入った問題は、まず N=1,2,3 で実験です。

• 1秒後： Pの隣の部屋にいるため、Qにはいない（確率0）。
• 2秒後： P、またはPの隣の隣の部屋にいるため、Qにはいない（確率0）。
• 3秒後： Pの隣の隣の隣の部屋にいるため、Qにいる可能性がある（確率 > 0）。

この実験から、Nの偶奇性が解答を大きく分けることが分かります。

また、図の対称性から、Qと左右対称の位置にある部屋（左下の部屋）の確率は常にQと同じになります。

2. 偶奇性で問題を分割

法則性が見つかったので、これで問題を大きく分割します。

ケース1：Nが奇数の時

PからQへ移動するには、縦に3回、横に3回、計6回の移動が必要です。PからQまでの最短移動回数は6回です。

奇数回（1回、3回、5回…）の移動では、PとQの位置関係から、Qに到達することは絶対に不可能です。

よって、N が奇数の時、Qにいる確率は 0 です。[47:11]

ケース2：Nが偶数の時（N=2m）

N が偶数の場合は、Qにいる可能性があります。確率を考えるために、再び「場合分けをする」を実践し、漸化式を立てて問題を分割します。

• Pm​：2m 秒後にPにいる確率
• Qm​：2m 秒後にQにいる確率（対称な部屋も Qm​）
• Rm​：その他の部屋にいる確率（ここでは簡略化し Rm​ は Pm​,Qm​ 以外の部屋の確率の和として扱う）

2(m+1) 秒後の確率を、2m 秒後の状態から考え、漸化式を導出します。

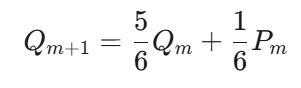
3. 忘れがちな条件による問題の分割（全確率の利用）

ここで、分母の違う3つの確率（Pm​,Qm​,Rm​）を使うと、連立漸化式になり計算が複雑になります。

ここで、確率問題で最も忘れがちな「全確率の和が1」という条件を思い出します。

全事象の確率は1なので、全ての部屋の確率の和は 1 です。

Pm​+Qm​+Qm​+Rm​+⋯=1

対称性を利用すると、確率は Pm​ と Qm​ に集約できることが実験から示唆されるため、部屋全体の状態の和は、以下の式で近似できると推測します（実際の東大の解答では厳密な定義が必要ですが、授業ではこれを活かします）。

​と仮定し代入

この関係式を漸化式に代入することで、連立漸化式を回避し、Qm​ だけの簡単な漸化式に帰着できます。[

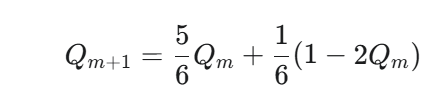
これを整理すると、

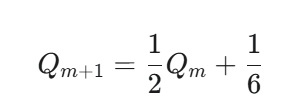
等比数列の形（特性方程式 α=21​α+61​ より α=31​）に帰着できたため、容易に解くことができます。

ここで Q0​（0秒後にQにいる確率）は0なので、

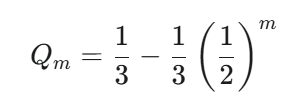
最後に m=N/2 に戻して、答えが導出されます。

教訓： 文字の多さに惑わされず、まずは簡単な場合で法則性を探すこと。そして、当たり前すぎて見落としがちな**「全事象の確率の和は1」という条件も、立派な問題を分割し、単純化する武器**になるのです。

思考法・メンタル面：知識より大切な心構え

最後に、先生は知識の量よりも遥かに重要な心構え、そして入試本番で使えるメンタル面の最終奥義について語っています。

心構えの転換が点数を変える

先生が自身の英語学習の経験から得た教訓があります。単語や文法を詰め込んでも英文が読めなかった時期、**「ミステリー小説を読む時のように、次を予測しながら読む」**という心構えに変えた途端、一気に読解力が向上したと言います。

これは数学でも全く同じです。

• 「場合分けをさせられる」（受動的な心構え）
• 「場合分けを自らする」（能動的な心構え）

この考え方の転換こそが、皆さんの知識を「使える武器」に変える、最も本質的な変化なのです。知識を詰め込んだ瞬間よりも、その知識を使う方法が確立した瞬間に、点数は大きく変わります。

メンタル面の最終奥義（俯瞰的な視点）

入試本番の極度の緊張状態の中で、上記の実践テクニックを試してもなお、本当に何もアイデアが浮かばない時のための、最後の秘策です。

それは、**「目をつぶり、尊敬する先生を頭に浮かべる」**ことです。

• まず目をつぶり、一呼吸置く。
• 自分よりも数学ができる尊敬する先生を頭の中に呼び出す。(例：ガウス）
• そして、**「もしこの先生が、この問題を今、目の前で解説するとしたら、どういう説明から始めるだろうか？」**と、俯瞰的な視点で考えてみるのです。

自分が主役になっていると、緊張で視野が狭まり、視野がロックされます。しかし、頭の中で先生に解説してもらうことで、「ああ、まず具体例で実験しろって言ってたな」といった、授業で学んだ思考のプロセスが、冷静さを取り戻した頭に蘇ってくることがあります。

このテクニックは、本番でこそ絶大な効果を発揮します。

まとめ：あなたの数学力は、考え方で決まる

今回の特別授業で学んだ、入試数学における対処法をまとめます。

1. 【原則】解かない（捨てる）：全問正解は不要。解けない問題は潔く捨て、解ける問題に集中する。
2. 【実践】具体例で考える：文字を具体的な数に置き換え、手を動かし、法則性を探す。
3. 【実践】問題の分割を望む：場合分けを歓迎し、問題を分割して解ける部分を意図的に増やし、部分点を掴む。
4. 【心構え】知識よりも考え方：能動的な心構えに転換し、知識を「使える武器」にする。

受験生の皆さん、あなたが今持っている知識は、時間をかけて積み重ねた努力の結晶です。その努力を本番で最大限活かすために、必要なのはさらなる知識の詰め込みだけではありません。

「全く分からない問題」に遭遇したとき、どう考え、どう行動するか。

この思考の技術こそが、あなたの数学力をグッと高め、合格へと導く鍵となるでしょう。入試本番で「困ったな」と思ったら、ぜひこの3つの対処法を思い出して、冷静に問題に立ち向かってみてください。

無料受験相談も実施中

現論会の受験相談はいつでも無料で、受け付けておりますので、お電話やHPの「無料受験相談」から気軽にお問い合わせください！

現論会は、東大・京大・医学部・早慶上理・GMARCHなどの難関大学合格者である凄腕の専属コーチが、独自の学習コーチングで生徒の大学受験勉強を全力でサポートする学習塾です。難関大学受験を乗り越えたコーチたちが、個々の生徒に応じてオーダーメイドで1日単位で学習計画を作成いたします！南浦和で大学受験に対応した塾をお探しの際は是非、南浦和駅から徒歩2分の埼玉県さいたま市にある現論会南浦和校をご利用ください。