知らないと「マジで」大損するかも!モンティ・ホール問題で体感する「確率のズレ」
更新日 : 2025年11月19日
3つのドアのうち1つに当たりが入っている。
あなたが1つ選んだ後、司会者がハズレのドアを1つ開ける。
残り2つのうち、選び直した方が当たりやすいのか?
これは知識ではなく、確率の理解を診断するテストです。
スクロールすると答えがあるので、答えを決めたら下に移動してみてください。
モンティ・ホール問題の正答率
一般的な統計:
正答率 10〜15%(9割近くが“直感”で不正解)
【問題】モンティ・ホール問題
3つのドアのうち1つに当たりが入っている。
あなたは1つのドアを選ぶ。
司会者は、選ばれなかったドアのうち、ハズレ1つだけを必ず開ける。
残ったドアは2つになった。
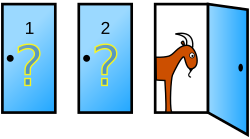
問1:次のうち、当たりを引ける確率が最も高い行動を1つ選びなさい。
1 最初の選択を変えない
2 もう一方のドアに選択を変える
3 どちらでも確率は同じ
▶ 答え↓
正解:2. もう一方のドアに選択を変える
【解説】なぜ確率が変わるのか
最初に引いたドアが
当たりである確率は1/3。
外している確率は2/3。
司会者はハズレだけを必ず開けるため、
最初に外していた確率2/3が、そのまま残ったドアに集中する。
つまり
選択を変えない場合:1/3
選択を変える場合:2/3
この差が生まれる。
確率直感のズレはなぜ起こる?
人は「残った2つだから1/2だ」と考えやすい。
しかし、“司会者がハズレを必ず開ける”という条件は、
単純な1/2にはならない。
条件を正確に読む。
与えられたルールの影響を考える。
直感より計算を優先する。
この3つが確率では不可欠になる。
数学の力を「思い込み」から救い出す
数学が伸びない原因の多くは、計算力ではなく
問題文の条件を正確に読み取れないことにある。
・「等しい」のか
・「必ず」のか
・「場合がある」のか
・「確率に影響する操作」なのか
・「観測の仕方が変わっている」のか
これらを読み間違えると、どんなに計算ができても正答にならない。
モンティ・ホール問題は、
“直感が間違える”
“条件が確率を動かす”
という数学の本質を短い文章の中で体験できる。
現論会のコーチングでは、こうした「読み取りのズレ」を一つずつ修正し、
確率・整数・文章題を安定して解ける状態を作る。
確率が苦手な人は公式の頼るからであり、状況をちゃんと理解するところから始めよう。
