模試の偏差値って何? 何が危険?
更新日 : 2025年11月18日
偏差値という数字は多くの受験生の心を揺さぶる数値です。上がると安心し、下がると不安になります。けれど、この数値を正しく理解していないと勉強の舵取りを誤ります。ここでは数学的な定義から、現実の模試で起こっていること、海外の指標との違い、そして受験生が実際にどう使えばよいかまで、丁寧に整理します。
偏差値の数学的な意味
偏差値は標準化という統計操作の一種です。テストの素点が平均何点で、点数のばらつきがどれくらいかを用いて、個々の得点を共通の物差しに載せ替えます。
計算の流れは次の通りです。
1 平均点を引く
2 標準偏差で割る
3 使いやすいように平均50、標準偏差10のスケールに線形変換する
この結果、偏差値50は集団の平均、60は平均よりちょうど標準偏差1個分上、40は1個分下を表します。分布が理想的に釣り鐘型に近いと仮定すれば、偏差値60以上は全体の上位約16パーセント、70以上は上位約2パーセントという目安が使えます。
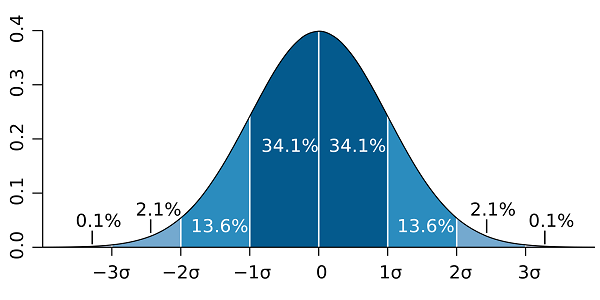
(釣鐘型のイメージ 引用:http://blog.ac.eng.teu.ac.jp/blog/2023/08/post-78e026.html)
暗黙の前提
偏差値という道具を当てはめるとき、いくつかの前提を置いています。ここが崩れると読み方も変わります。
1 分布が釣り鐘型に近いこと
極端に易しすぎるテストや難しすぎるテストでは点が端に寄り、釣り鐘型から外れます。満点続出や白紙続出のような状態では、そもそも点数の分布が上記のような構造になっていないので、偏差値という数字が意味をなさなくなります。
2 受験者集団が比較可能であること
同じ模試名でも回によって受験者の顔ぶれが違います。ハイレベル層が多い回では同じ素点でも偏差値は下がりやすく、逆もまた然りです。
3 同一テスト内での比較であること
国語の偏差値と数学の偏差値を足したり、模試Aと模試Bの偏差値を横比較したりしても意味が異なります。異なる設計思想、採点設計、受験者層が混ざるからです。
海外では何を使っているか
海外では偏差値というラベルはほぼ使いません。使っている概念は偏差値と同根ですが、表記や運用が異なります。
1 百分位
同じスコアが全体の上位何パーセントかを示す指標です。直感的で入学選考の資料に用いられます。
2 標準得点
zスコアやtスコアの形で学力検査の結果を標準化します。米国の心理検査や教育測定では一般的です。
3 スケールドスコア
SATやACTはテストごとの難易度差を補正して共通スケールに変換した点数を公表します。偏差値のように他者と比較する数字ではなく、同じ試験体系内で縦比較するための数字です。
4 グレード制
英国のGCSEやAレベル、日本の共通テストの一部判定のように段階評価を主に用い、詳細な序列化は避ける設計もあります。
つまり、世界的には相対指標は使いつつも、入試は複数の証拠を束ねて見る方向が主流です。偏差値一本で合否を決める文化は限定的です。
偏差値を誤読しやすいポイント
ここは特に注意してほしい場所です。
1 偏差値至上主義
偏差値の上下に感情が引っ張られ、学習行動がぶれる現象です。偏差値は結果の要約であり、原因は答案にあります。原因に戻れないと改善は起きません。
2 科目間比較の罠
同じ回の英語60と数学50を並べて英語得意と結論付けるのは早計です。科目固有の分布、設問設計、解き方のフィットが影響します。答案の中身を見て初めて意味が出ます。
3 小標本のゆらぎ
受験者が少ない地方模試や学校模試では標準偏差の推定が不安定になり、偏差値が跳ねます。数字の桁が整っていても誤差は現実に存在します。
4 回またぎの単純比較
模試Aの60と模試Bの60を同じ強さと見なすのは危険です。追うべきは同一シリーズ内の時系列、同一科目、同一設計の数字です。
5 回答戦略の影響
同じ実力でも、見直し配分や捨て問の判断で偏差値は動きます。学力だけの指標ではなく、戦略や体調も混ざっています。
6 平均回帰の見落とし
一回急伸した後に戻る、下がった後に戻るという現象は統計的に自然です。一本の線ではなく帯で実力を捉えてください。
数字に強くなるためのミニ例題
次の2つの模試であなたはどちらも70点を取りました。
模試A 平均50点 標準偏差10点
模試B 平均60点 標準偏差5点
Aでは平均から20点上で標準偏差2個分。Bでは平均から10点上で標準偏差2個分。どちらも偏差値はほぼ同程度になります。同点でも集団のばらつきが違えば相対位置が変わるということです。素点だけで優劣は決まりません。
偏差値を味方にする実践手順
数字に振り回されず、数字を使いこなすための手順を示します。
1 目的を定める
志望校の科目配点、本番の形式、合格可能性に対して何を測りたいのかを先に決めます。偏差値はその目的に対する中間指標です。
2 同一シリーズを時系列で追う
同じ模試、同じ学年対象、同じ科目で推移を見るのが基本です。三回連続のトレンドに意味が出ます。
3 偏差値より誤答分析を優先する
落とした設問のタイプ、根拠の欠落、計算の癖、語彙の穴を分類します。偏差値は結果、改善の出発点は誤答です。
4 学習戦略に接続する
誤答から直結する教材と行動を決めます。次回模試の日付をゴールに、週単位の練習計画に落とし込みます。
5 数字のブレ幅を前提にする
一本の線ではなく帯で自分の実力を捉えます。例えば英語は偏差値58から62の帯、といった見方をします。
6 科目横断での資源配分
帯の位置と志望校配点から、時間配分を最適化します。伸びしろが大きく配点も重い科目へ資源を寄せるのが基本です。
まとめ
偏差値は便利な要約です。しかし、それは分布と受験者層という文脈の上でのみ意味を持ちます。海外でも標準化得点や百分位は使いますが、偏差値そのものを唯一の学力指標に据える文化は一般的ではありません。大切なのは、数値に一喜一憂することではなく、数値の裏側にある自分の思考と答案を読み解くことです。
数字は道具です。道具を正しく握れば、進む方向が見えます。偏差値を成果の指標ではなく、改善の地図として使いこなしましょう。
